Tree in Data Structure using C#

Question

In this post, we will explain What's Tree in Data Structure?, and What're Tree types?, and How Tree works using C#?.

It’s recommended to read what is data structure?

What is Tree in Data Structure?

A Tree is a non-linear data structure that represents the nodes connected by edges, node it’s like an item or element in an Array which contains data. 

Key points of Tree in Data Structure

Let’s understand the key points of the tree and make the picture clear.

• A tree data structure is defined as a collection of objects or entities known as nodes that are linked together to represent or simulate hierarchy.
• A tree data structure is a non-linear data structure because it does not store in a sequential manner.
• The topmost node is known as a root node. Each node contains some data, and data can be of any type. 

Tree Terminologies in Data Structure

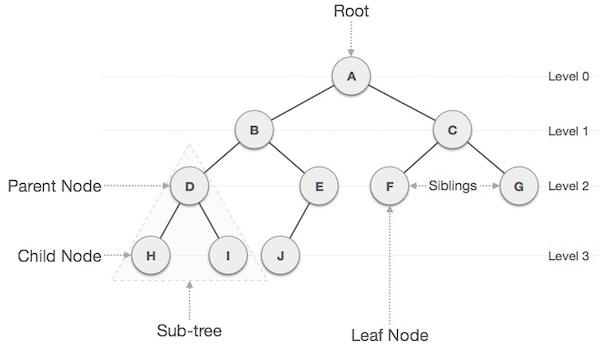
The tree has many terminologies and the below image and table clarifies the basics for each terminology with a detailed definition and example

Terminology	Definition	Example from the image
Root	The node at the topmost of the tree, and does not have a parent.	Node A.
Parent Node	Any node has one edge and upward to a node except the Rood node.	Node {B, C, D, E} are parents.
Child Node	The node is downward of any node.	Node {D, E} are children of B.
Leaf	The node that does not have any child node.	Node {H, I, J, F, G} are all leafs.
Edge	The connection between one node to another. It’s a line between two nodes.	The line between B and D, A and C.
Siblings	The nodes with the same parent.	Node {F, G}, {H, I} are siblings.
Sub-tree	The parent node and his children this called sub-tree.	Node {D, H, I}, {C, F, G} are sub-tree.
Depth	The count of edges from the root to the node.	Depth(H)= 3, depth(C)= 1.
Height	The number of edges on the longest path from that node to a leaf. If you want the height of the tree it’s the height of the root.	Height(B)= 2, Height(A)= 3
Ancestor	Any predecessor node on a path from the root to that node. The root node doesn't have any ancestors.	Ancestor(H)= D, B, A. Ancestor(E)= B, A.
Level of node	The count of edges on the path from the root node to that node. Allows root in level zero.	{B, C}= level 1, {D, E}= level 2
Keys	The value of a node based on which a search operation is to be carried out for a node.	The key root is A.

You have to match each terminology in a table with its corresponding in the image to get well understanding for most of all the terminology of the tree.

---

Type of tree Data Structure

In this section, we will learn what are the types of trees in the data structure, and we will also cover the Binary tree and we will dig deeper into its types.

The main types of the tree are:

• Binary tree.
  1. Binary Search Tree.
  2. AVL Tree.
• B tree.
• Multiway tree.
• Application-specific tree.

There are a lot of types in a tree, and some people become nervous about these types and have questions like, Is binary search tree or AVL tree is one of the types?

The answer is no, because the binary search, AVL are types that come under the Binary tree.

In the next section, we will clarify that and we will explain the types of binary trees each of them one by one, but first, we will explain the General tree and the binary tree then have a brief of it.

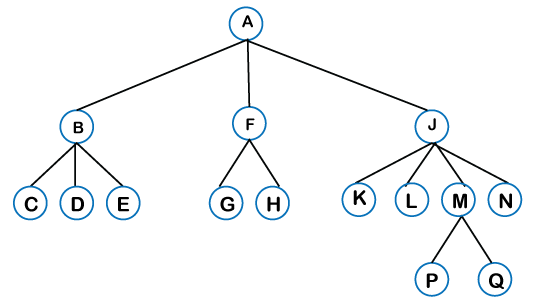
1) General Tree

In the general tree, a node can have either 0 or maximum n number of nodes. There is no restriction imposed on the degree of the node (the number of nodes that a node can contain).

The image below makes the picture clear.

2) Binary Tree

In the binary tree, each parent node can have at most two children.

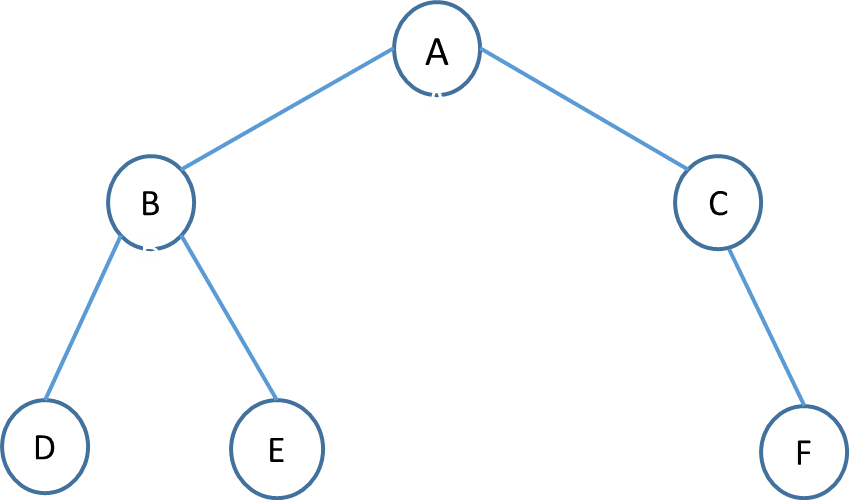
Binary trees are further divided into many types.

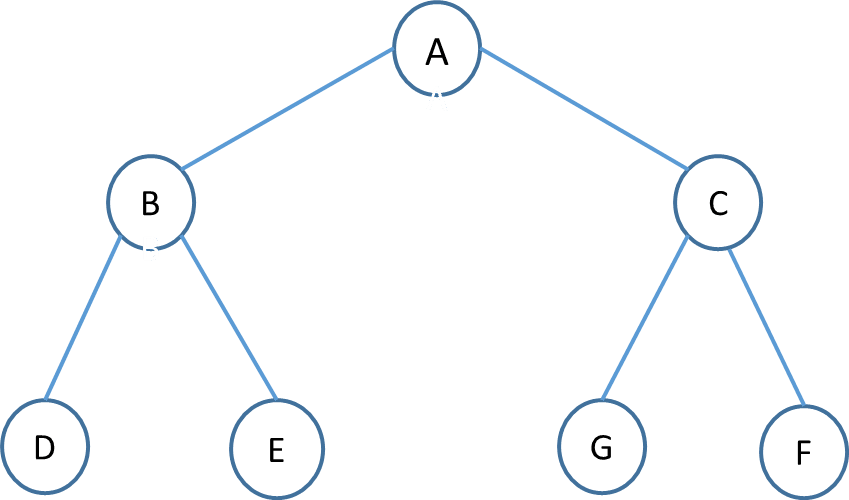
1. Full Binary Tree: If every node in a tree has either 0 or 2 children, then the tree is called a full tree.
2. Perfect Binary tree: It is a binary tree in which all interior nodes have two children and all leaves have the same depth or same level.

To know the perfect binary tree, you need to know the leaves and nodes in the tree, l = 2h and n = 2^h+1 – 1 where n is a number of nodes, h is the height of the tree and l is a number of leaf nodes.

In the below diagram, h is 2 so leaves will be 4, and nodes will 2^3–1 which is 7.

3) Binary Search Tree

A binary search tree (BST), follows some order to arrange the elements. In a Binary search tree, the value of the left node must be smaller than the parent node, and the value of the right node must be greater than the parent node.

Let's understand the concept of a Binary search tree with an example.

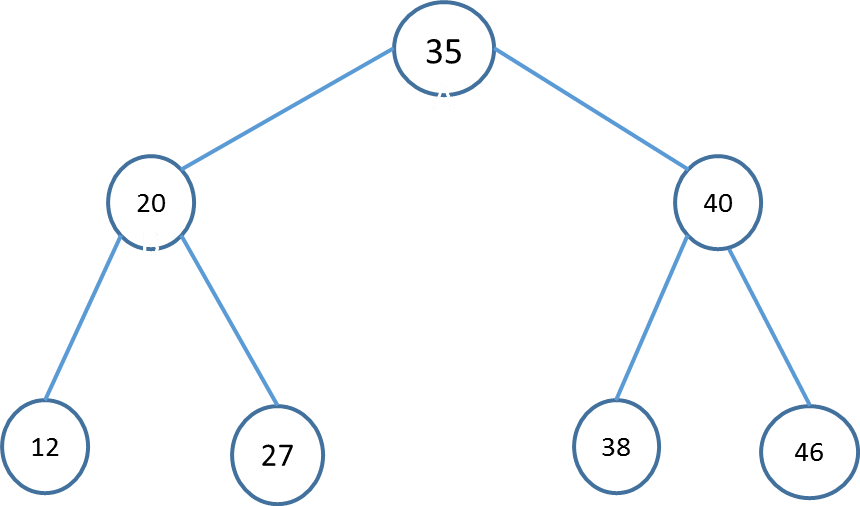
• In the above image, the root node is 35, all the nodes of the left subtree are smaller than the root, and all the nodes of the right subtree are greater than the root.
• Similarly, we can see the left child of the root node is greater than its left child and smaller than its right child. Know we can say the tree is a binary search.

What makes BST have an advantage that is the search in the tree is so much easy as we always have a hint that which subtree has the desired element.

you can visualization the binary search tree in the this Data Structure Visualizations

3. AVL Tree

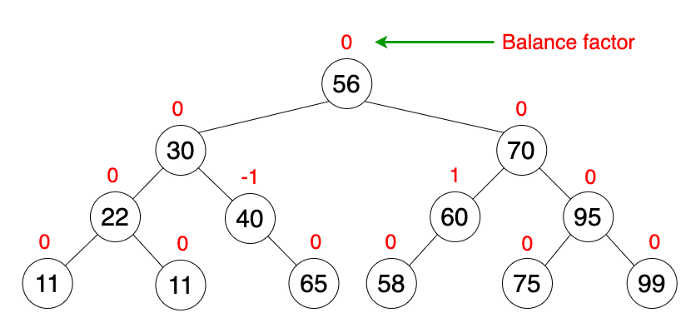
AVL tree is a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees cannot be more than one for all nodes.

AVL Tree Properties

There is a property to understand the AVL tree.

• Self-balancing.
• Each node stores a value called a balance factor which is the difference in height between its left subtree and right subtree.
• All the nodes must have a balance factor of {-1, 0, 1} otherwise, the tree will be unbalanced and need to be balanced.

The image below explains AVL with a balancing factor.

You can visualization the AVL tree at Data Structure Visualizations.

---

How does Tree work in Data Structure?

In this section, we will explain how binary search tree works in the data structure and there are three main operations:

1. Insertion operation
2. Search operation 
3. Deletion operation

1) Insertion operation

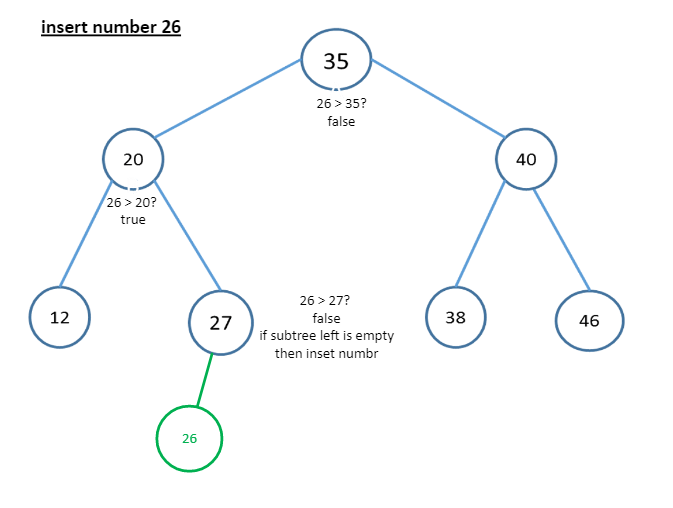
To add an element to the binary search tree you need to use insert operation and there are steps to insert:

1. Locate its proper location.
2. Start searching from the root node
3. If the data is less than the key value search for the empty location in the left subtree and insert.
4. If else search for the empty location in the right subtree and insert.

Below the image, we have an example for inserting the number 26 in the Tree.

2) Search operation

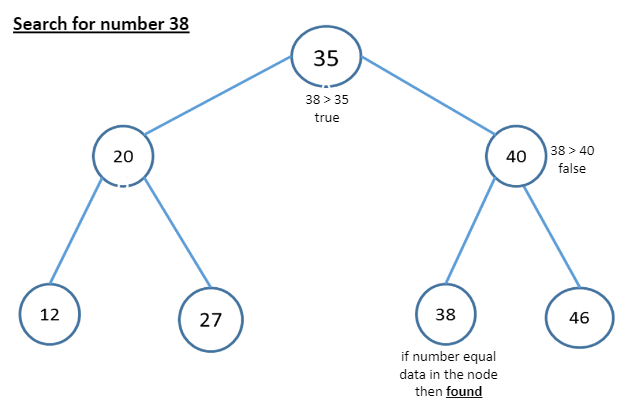
We will use the same way in insert operation to understand the Search operation and we will explain the operation step by step.

1. Start searching from the root node.
2. If the data is less than the key value search for the element in the left subtree.
3. If else search for the element in the right subtree.
4. If we don’t find the element then return null.

Below the image, we have an example for searching for the number 38 in the tree.

3) Deletion operation

In the deletion operation, there are three cases and we will explain each of them one by one:

Case one:

• Deleting a node with no children: remove the node from the tree.

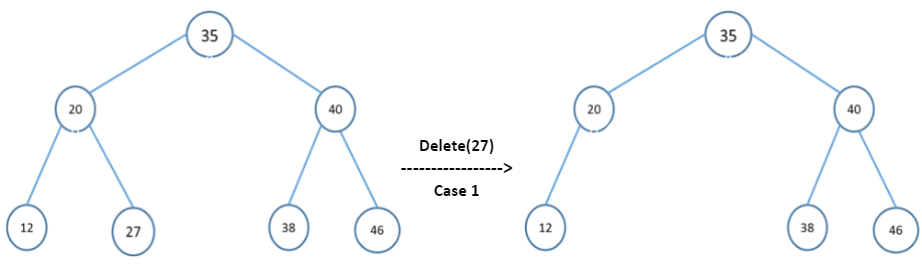
Case two:

• Deleting a node with one child: remove the node and replace it with its child.

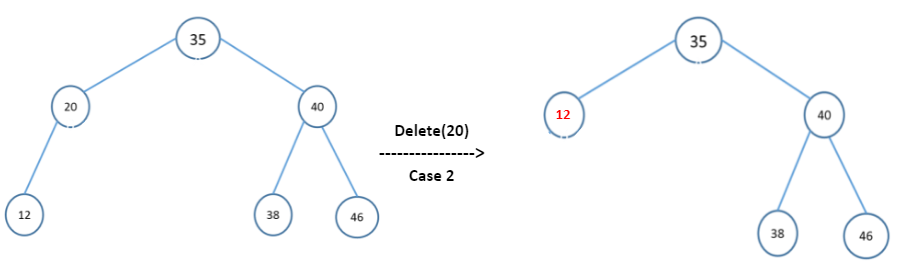
Case three:

• Node has two children and this case is the most complex of the three cases we will explain below.
  1. Call the node to be deleted N. Do not delete N. Instead,
  2. Choose either its in-order successor node or its in-order predecessor node, R.
  3. Copy the value of R to N, then recursively call delete on R until reaching one of the first two cases.
  4. If we choose the in-order successor of a node, as the right subtree is not NULL, then its in-order successor is a node with the least value in its right subtree, which will have at a maximum of one subtree, so deleting it would fall in one of the first two cases.

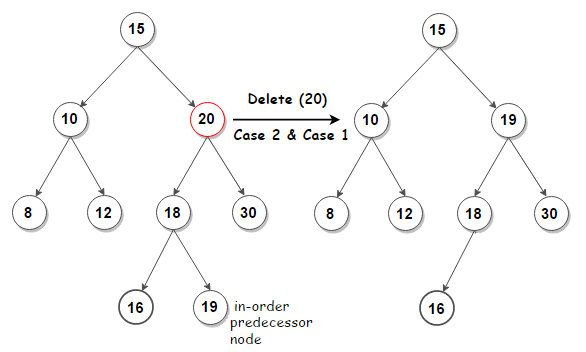
Example: Implementing Code of the binary search tree in C#

In this example, you will learn how to create a tree and insert a node into it, delete a node, and print all the nodes in the tree.

First, create node class & Root & Constructor.

/* Class containing left and right
child of current node and key value*/

class Node
{
    public int key;
    public Node left, right;

    public Node(int item)
   {
      key = item;
      left = right = null;
   }
}

// Root of BST
Node root;

// Constructor
BinarySearchTree() { root = null; }

Second create functions

1. MinValue()

// this method return the minimum value in the tree
int MinValue(Node root)
{
    int minValue = root.key;
    while (root.left != null)
    {
        minValue = root.left.key;
        root = root.left;
    }
    return minValue;
}

2. DeleteKey() & DeleteRec()

// This method mainly calls DeleteRec()
void DeleteKey(int key) { root = DeleteRec(root, key); }

/* A recursive function to
  delete an existing key in BST
 */

Node DeleteRec(Node root, int key)
{
    /* Base Case: If the tree is empty */
    if (root == null)
        return root;

    /* Otherwise, recur down the tree */
    if (key < root.key)
        root.left = DeleteRec(root.left, key);
    else if (key > root.key)
        root.right = DeleteRec(root.right, key);

    // if key is same as root's key, then This is the
    // node to be deleted
    else
    {
        // node with only one child or no child
        if (root.left == null)
            return root.right;

        else if (root.right == null)
            return root.left;

        // node with two children: Get the
        // inorder successor (smallest
        // in the right subtree)
        root.key = MinValue(root.right);

        // Delete the inorder successor
        root.right = DeleteRec(root.right, root.key);
    }
    return root;
}

3. Insert() & InsertRec()

// This method mainly calls insertRec()
void Insert(int key) { root = InsertRec(root, key); }

/* A recursive function to insert a new key in BST */
Node InsertRec(Node root, int key)
{

    /* If the tree is empty, return a new node */
    if (root == null)
    {
        root = new Node(key);
        return root;
    }

    /* Otherwise, recur down the tree */
    if (key < root.key)
        root.left = InsertRec(root.left, key);
    else if (key > root.key)
        root.right = InsertRec(root.right, key);

    /* return the (unchanged) node pointer */
    return root;
}

4. Inorder() & InorderRec()

// This method mainly calls InorderRec()
void Inorder() { InorderRec(root); }

// A utility function to do inorder traversal of BST
void InorderRec(Node root)
{
    if (root != null)
    {
        InorderRec(root.left);
        Console.Write(root.key + " ");
        InorderRec(root.right);
    }
}

The third is the main method:

public static void Main(String[] args)
{
    BinarySearchTree tree = new BinarySearchTree();

    /* Let us create following BST
                50
            /  \
            30    70
            / \    / \
        20 40  60 80 */
    tree.Insert(50);
    tree.Insert(30);
    tree.Insert(20);
    tree.Insert(40);
    tree.Insert(70);
    tree.Insert(60);
    tree.Insert(80);


    Console.WriteLine(
        "Inorder traversal of the given tree");
    tree.Inorder();

    Console.WriteLine("\nDelete 20");
    tree.DeleteKey(20);
    Console.WriteLine(
        "Inorder traversal of the modified tree");
    tree.Inorder();

    Console.WriteLine("\nDelete 30");
    tree.DeleteKey(30);

    Console.WriteLine(
        "Inorder traversal of the modified tree");
    tree.Inorder();

    Console.WriteLine("\nDelete 50");
    tree.DeleteKey(50);

    Console.WriteLine(
        "Inorder traversal of the modified tree");
    tree.Inorder();
}

Output

Inorder traversal of the given tree
20 30 40 50 60 70 80
Delete 20
Inorder traversal of the modified tree
30 40 50 60 70 80
Delete 30
Inorder traversal of the modified tree
40 50 60 70 80
Delete 50
Inorder traversal of the modified tree
40 60 70 80

You can find the source code for this example at GitHub

---

References

• introduction to tree data-structure - geeksforgeeks
• tree - javaTpoint

See Also 

• What is Queue and How to use it in C#?
• How to use Stack in C#?
• How to use Linked List in C#?
• How to use Array in C#?