In this article, you will learn what a Graph Data Structure is. Also, you will find representations of a Graph, the types, and applications of the Graphs. Moreover, breadth-first search (BFS) and how it works will be explained thoroughly.
It’s recommended to read what is data structure first.
What is Graph in Data structure?
A Graph is a non-linear data structure like a Tree, and it is a collection of nodes that are connected to other nodes by edges.
The nodes are sometimes also referred to as vertices and the edges are lines that connect any two nodes or vertices in the Graph. Take a look at the following Graph.
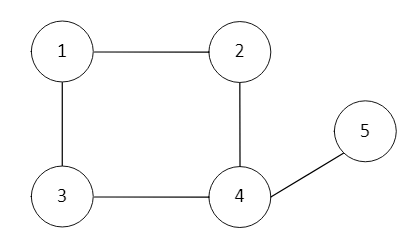
In the above Graph, we have vertices that contain the data (number) and the edges are connecting between the vertices. We can say a Graph is a pair of sets (V, E) where V is vertices and E is an edge connecting the pairs of vertices.
V = {1, 2, 3, 4, 5} //we have 5 Vertices.
E = { (1, 2), (1, 3), (2, 4), (4, 3), (4, 5) } //we have 6 Edges.
G = {V, E} // the Graph
Graph Representation
We can represent Graph in two different ways:
1) Adjacency Matrix
An adjacency matrix is a 2D array. Each row and column represent a vertex.
If the value of any element a[i][j] is 1, it represents that there is an edge connecting vertex i and vertex j.
The adjacency matrix for the Graph in the diagram above is.
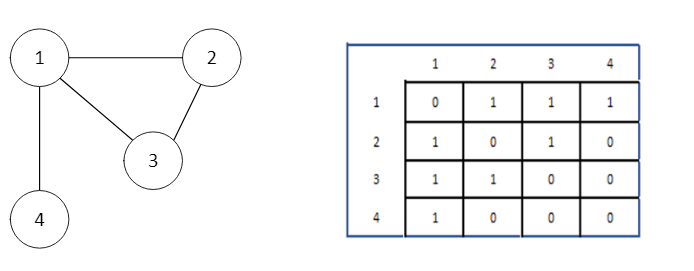
Since it is an undirected Graph, for edge (1,3) we also need to mark edge (3,1) making the adjacency matrix symmetric about the diagonal.
2) Adjacency List
An adjacency list represents a Graph as an array of linked lists.
The index of the array represents a vertex and each element in its linked list represents the other vertices that form an edge with the vertex.
The adjacency list for the Graph in the diagram above is.
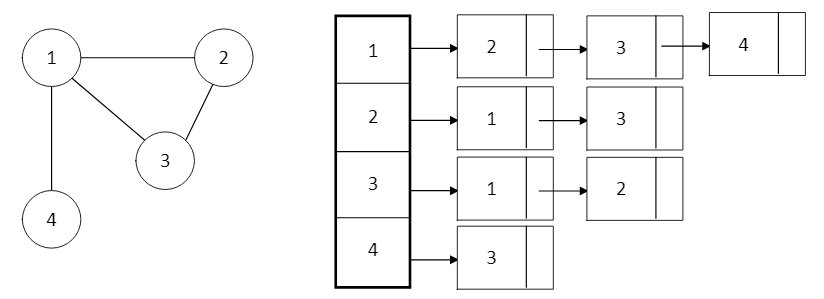
An adjacency list is efficient in terms of storage because we only need to store the values for the edges. And this way is useful when we have a lot of vertices like millions.
Types of Graphs in Data Structure
There is a lot of types but here we will mention the popular types.
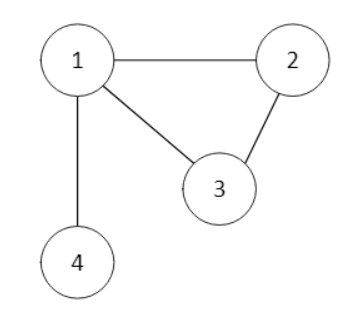
1) Undirected
A Graph in which all the edges do not point in a specific direction.
2) Directed
A Graph in which all the edges are pointed in a single direction.

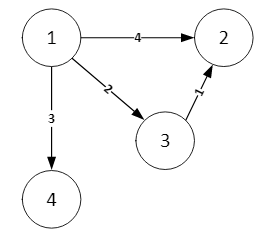
3) Weighted Graph
A Graph that has a value associated with every edge. The values corresponding to the edges are called weights. A value in a weighted Graph can represent things depending on what you will use such as distance, and time.
Application of Graph in Data Structure
Graphs have a lot of applications. And below we will mention the most popular applications:
- Used in social networks such as Facebook and Linkedin. In Linkedin, it’s suggested to follow x, because x is your friend's follower. And Linkedin knew this relationship by the Graph.
- Used in Google maps for building transportation systems. In google maps, the intersection of two or more roads represents the vertex while the road connecting two vertices represents an edge.
- Used in the World Wide Web where the web pages represent the nodes.
Traversal means to visit each node of a Graph. For Graphs, there are two types of traversals:
- Depth First traversal.
- Breadth-First traversal.
In this section, we are going to learn Breadth-first traversal/Search or BFS in detail.
What is Breadth-First Search (BFS)?
BFS is an algorithm for searching used in Tree and Graph. Breadth-First Search is a traversal technique in which we traverse all the nodes of the Graph in a breadth-wise motion. In BFS, we traverse one level at a time and then jump to the next level.
In a Graph, the traversal can start from any node and cover all the nodes level-wise. The BFS algorithm makes use of the queue data structure for implementation.
Graphs may contain cycles, so we may come to the same node again. To avoid processing a node more than once, we use a boolean visited array
How does BFS work?
To understand how BFS works, there are rules:
- Visit the adjacent unvisited vertex. Mark it as visited. Display it. Insert it in a queue.
- If no adjacent vertex is found, remove the first vertex from the queue.
- Repeat Rule 1 and Rule 2 until the queue is empty.
We will dig deeper into these rules by taking an example and explaining the example step by step.
Step 1
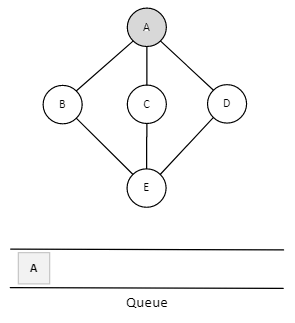
Consider we have the following Graph having 5 vertices {A, B, C, D, E}. and we have Queue.
Step 2
We start by visiting A (starting node), marking it as visited, and also enqueue it.
Step 3
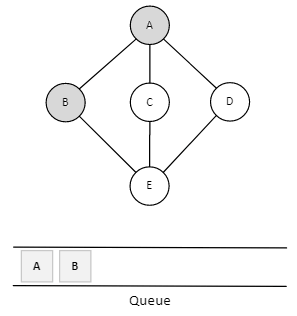
We then see an unvisited adjacent node from A. In this example, we have three nodes it does not matter choose anything, we choose B, mark it as visited, and enqueue it.
Step 4
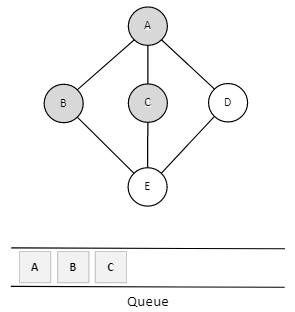
Next, the unvisited adjacent node from A is C. We mark it as visited and enqueue it.
Step 5
Next, the unvisited adjacent node from A is D. We mark it as visited and enqueue it.
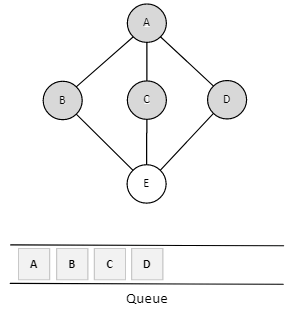
Step 6
Now, A is left with no unvisited adjacent nodes. So, we dequeue and find B.
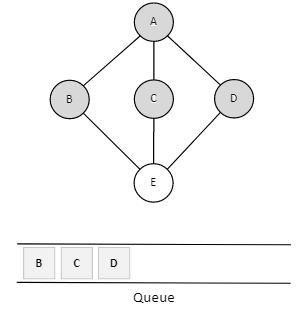
Step 7
From B we have E as an unvisited adjacent node. We mark it as visited and enqueue it.
By doing that we have all the vertices are visited.
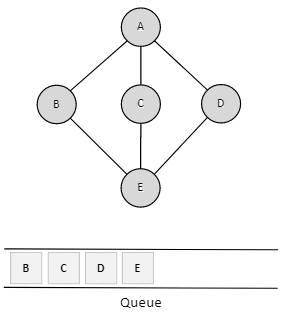
You can visualization the BFS at Data Structure Visualizations
Example: Implementing Code of the Breadth-First Search in the Graph using C#
In this example, you will learn how to create a Graph and add vertices with their edges, traversal each vertex, and print it using BFS.
class Graph
{
// No. of vertices
private int _V;
//Adjacency Lists
LinkedList<int>[] _adj;
public Graph(int V)
{
_adj = new LinkedList<int>[V];
for (int i = 0; i < _adj.Length; i++)
{
_adj[i] = new LinkedList<int>();
}
_V = V;
}
// Function to add an edge into the graph
public void AddEdge(int v, int w)
{
_adj[v].AddLast(w);
}
// Prints BFS traversal from a given source s
public void BFS(int s)
{
// Mark all the vertices as not visited
bool[] visited = new bool[_V];
for (int i = 0; i < _V; i++)
visited[i] = false;
// Create a queue for BFS
Queue<int> queue = new Queue<int>();
// Mark the current node as
// visited and enqueue it
visited[s] = true;
queue.Enqueue(s);
while (queue.Any())
{
// Dequeue a vertex from queue
// and print it
s = queue.First();
Console.Write(s + " ");
queue.Dequeue();
// Get all adjacent vertices of the
// dequeued vertex s. If a adjacent
// has not been visited, then mark it
// visited and enqueue it
LinkedList<int> list = _adj[s];
foreach (var val in list)
{
if (!visited[val])
{
visited[val] = true;
queue.Enqueue(val);
}
}
}
}
static void Main(string[] args)
{
Graph graph = new Graph(5);
graph.AddEdge(0, 1);
graph.AddEdge(0, 2);
graph.AddEdge(1, 2);
graph.AddEdge(2, 0);
graph.AddEdge(2, 3);
graph.AddEdge(3, 4);
Console.Write("Following is Breadth First Traversal(starting from vertex 2)\n");
graph.BFS(2);
}
}
output
Following is Breadth First Traversal(starting from vertex 2)
2 0 3 1 4
See Also
References